梯度增强树的实用指南-第一部分，回归gydF4y2Ba

MartinLiebiggydF4y2Ba

梯度增强树是最强大的分类和回归算法之一。它们具有树的所有优点，包括能够很好地处理标称数据。任何强大的多元方法的缺点是它的复杂性。这是深入研究算法并解释其工作原理的系列文章的第一篇。gydF4y2Ba

设置gydF4y2Ba

在本教程中，我们将研究梯度增强树是如何做回归的。作为训练数据，我们使用0到1之间的平方根函数。gydF4y2Ba

为了使我们的算法更容易理解，我们使用了一些简化。我们对标签变量(gydF4y2BaygydF4y2Ba)，只有一个因变量(gydF4y2BaxgydF4y2Ba）.gydF4y2Ba

我们确实使用深度为1和学习率为1的GBT。我们将在后面的文章中更深入地讨论这些选项。gydF4y2Ba

初始化gydF4y2Ba

在开始真正的算法之前，我们将设置一个基线预测。我们的整个算法由很多步骤组成。得到的函数f(x)近似于根号函数，它是各个步骤结果的和。第一步略有不同。我们设定基线预测fgydF4y2Ba0gydF4y2Ba到平均标签。在我们的数据中，这是0.667。gydF4y2Ba

现在我们可以开始第一次迭代了。gydF4y2Ba

步骤1 -计算错误gydF4y2Ba

作为第一步，我们计算误差。在我们的例子中，这些是我们之前的预测f(x)和真实y之间的残差。在我们的第一次迭代中，我们确实有f(x) = fgydF4y2Ba0gydF4y2Ba= 0.667。gydF4y2Ba

我们定义r = y - f(x)作为每个单独例子的误差。gydF4y2Ba需要注意的是，每次迭代中的树并不是预测标签，而是r!gydF4y2Ba由于这只是一个比例的变化，我们的平方根函数仍然是这样的:gydF4y2Ba

步骤2 -树的建设gydF4y2Ba

我们现在构建了一个预测r的回归树。由于我们将树的深度限制为1，我们得到:gydF4y2Ba

这棵树长出两片叶子。我们称它为叶向量RgydF4y2Ba11gydF4y2Ba和RgydF4y2Ba12gydF4y2Ba表示第一次迭代中的第一个和第二个叶。对于每一个叶结点我们都需要找到最好的预测。gydF4y2Ba

步骤3 -预测定义gydF4y2Ba

在我们的回归问题中，我们在叶中预测的计算是相当直接的。我们想要找到一个预测，它能使我们的函数和真实值之间的差异最小化。在我们的例子中，这是每叶上r的平均值。我们将第i次迭代中的预测和第j个叶子定义为ggydF4y2BaijgydF4y2Ba我们的数据是:gydF4y2Ba

ggydF4y2Ba11gydF4y2Ba= -0.254gydF4y2Ba

ggydF4y2Ba12gydF4y2Ba= + 0.157gydF4y2Ba

步骤4 -更新我们的功能gydF4y2Ba

现在我们可以更新我们的近似函数来估计y，称为f(x)。我们定义第一次迭代的结果fgydF4y2Ba1gydF4y2Ba：gydF4y2Ba

fgydF4y2Ba1gydF4y2Ba如果x < 0.382， = -0.254，否则:+0.152gydF4y2Ba

f(x) = fgydF4y2Ba0gydF4y2Ba+ fgydF4y2Ba1.gydF4y2Ba这将产生一个总函数，它近似于初始的未缩放平方根，如下所示:gydF4y2Ba

步骤1 -第二部分，再次建立剩余gydF4y2Ba

现在我们可以再次执行第一步。但这一次，我们建立了新函数f(x) = f之间的残差gydF4y2Ba1gydF4y2Ba+ fgydF4y2Ba2gydF4y2Ba和y，所以我们得到这样的图:gydF4y2Ba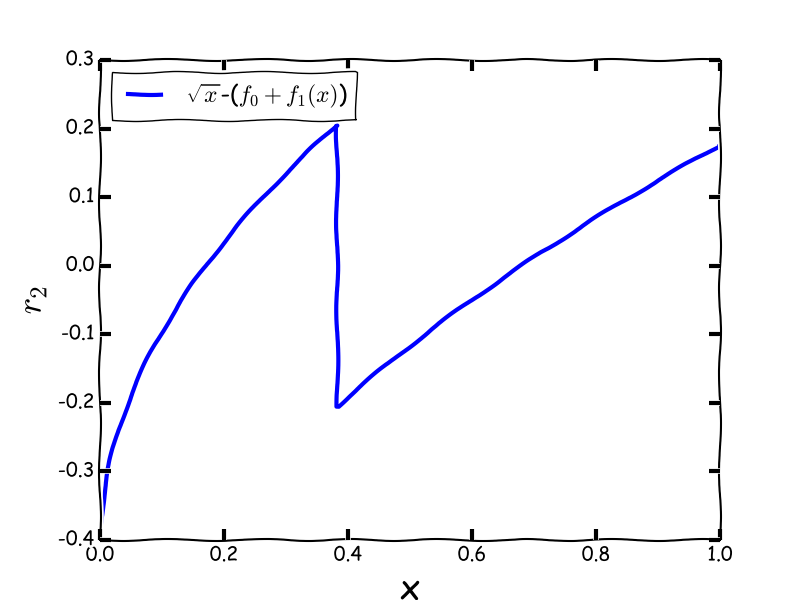

在此迭代算法中，我们尝试拟合残差函数，以获得更好的整体函数近似。gydF4y2Ba

步骤2和3-第2部分，建立树和计算预测。gydF4y2Ba

我们再次构建了一个树，将我们的数据分成不同的部分。如果你看上图，我们在x轴上搜索点，在那里我们可以画两条平行于a轴的直线，它们到残差的距离最小。gydF4y2Ba

这棵树告诉我们，分裂点在0.107处，两条平行线g21和g22分别是-0.193和+0.023。gydF4y2Ba

步骤4 -更新函数gydF4y2Ba

最后一步是更新我们的函数。现在是:gydF4y2Ba

F (x) = FgydF4y2Ba0gydF4y2Ba+ fgydF4y2Ba1gydF4y2Ba+ fgydF4y2Ba2gydF4y2Ba

或者用完整的话来说:gydF4y2Ba

fgydF4y2Ba1gydF4y2Ba= 0.667gydF4y2Ba

-0.254+如果x < 0.382gydF4y2Ba

如果x >= 0.382，则为+0.152gydF4y2Ba

- 0.193，如果x < 0.107gydF4y2Ba

如果x >= 0.107，则为+ 0.023gydF4y2Ba

或者画出来是这样的gydF4y2Ba

请注意，第二棵树也将函数的右边抬高了一点。gydF4y2Ba

有了这些知识，我们现在可以继续前进，重新开始第一步。就是这样。gydF4y2Ba

命名gydF4y2Ba

• ygydF4y2Ba是标签的值。例如，你想要预测的真实值gydF4y2Ba
• xgydF4y2Ba是因变量。例如，一个(或多个)规则属性gydF4y2Ba
• f (x)gydF4y2Ba推导的公式是用来预测的吗gydF4y2BaygydF4y2Ba．比如模型gydF4y2Ba
• RgydF4y2BaijgydF4y2Ba是算法第i次迭代中的第j个叶。gydF4y2Ba
• ggydF4y2BaijgydF4y2Ba对于第i次迭代和第j个叶的所有例子，将常数添加到函数中。注:文献中常称为gamma。gydF4y2Ba

phivugydF4y2Ba

感谢您对GBT算法的非常有用的一步一步的解释!gydF4y2Ba
在最后一步(步骤4 -更新函数)中是否有任何拼写错误?为什么条件重叠(x<0.382和x<0.107)?你能解释更多关于如何确定一个位置做一个分裂(在x= 0.382和x= 0.107)，或者f1和f2是如何构建的?gydF4y2Ba

Muhammed_Fatih_gydF4y2Ba

嗨gydF4y2Ba@mschmitzgydF4y2Ba，gydF4y2Ba

感谢你的有趣的指导如何梯度增强树的工作。非常有趣的!gydF4y2Ba

你这样写道:gydF4y2Ba

“重要的是要注意，每次迭代中的树不是预测标签，而是预测r!”gydF4y2Ba

这是否意味着在每次迭代中都考虑对各自r的预测，以计算最终由性能向量显示的总体性能(每次迭代中r的平均值)?gydF4y2Ba

或者性能向量是否代表树最终改进状态下的r预测?gydF4y2Ba

提前感谢您的反馈!gydF4y2Ba

最好的问候,gydF4y2Ba

FatihgydF4y2Ba

MartinLiebiggydF4y2Ba

嗨gydF4y2Ba@Muhammed_Fatih_gydF4y2Ba，gydF4y2Ba

我认为都不是。当你评估树的时候，你总是评估所有的树然后对每个结果求和。或者用数学方法来说:gydF4y2Ba

F (x) = \sum_i (f_i(x))gydF4y2Ba

我在不同的树上迭代。gydF4y2Ba

然后，性能向量总是在总和上计算，而不是在单个树上。gydF4y2Ba

如果你想更深入地了解它，请参阅Tibsharani, Hastie等人:gydF4y2Bahttps://web.stanford.edu/~hastie/Papers/ESLII.pdfgydF4y2Ba．这个指南基本上是我对书中章节的版本。gydF4y2Ba

最好的gydF4y2Ba

马丁gydF4y2Ba